この記事では、放射温度計を使った珈琲焙煎豆の温度測定とその光学系について記載しています。
珈琲焙煎と珈琲豆温度
私は珈琲が大好きで、それが高じて自家焙煎をするようになりました。珈琲豆を焙煎するには、珈琲の生豆(焙煎されていない豆)を使用します。それを加熱することで焙煎豆(焙煎された豆)となり,珈琲として飲めるようになります。焙煎には浅煎りや中煎り,深煎りと大雑把に3つの焙煎度があり、珈琲の味を左右します。焙煎度とは加熱量の大小による豆の化学反応の進行度合いを表します。簡単に言えば珈琲豆の加熱量のことです。それぞれの特徴をTable 1にまとめました。
Table 1 焙煎度による珈琲テイストの変化
| 浅煎り | 中煎り | 深煎り |
|---|---|---|
| 酸味とフレーバーが明るく フルーティーな飲み心地 | 酸味が薄れて 甘みとボディ感、苦味が明るくなる | 酸味は消え去り、 ボディ感と苦味が強くなる |
これを見ると、珈琲焙煎は珈琲の味を決定する重要な工程であることが分かります。焙煎工程を制御するパラメータとしては焙煎時間と焙煎温度が挙げられ、これら2つのパラメータのプロットしたグラフをFig.1に示します。このグラフは放射温度計による測定結果のため、温度が単調に増加しています。(焙煎でよく用いられる温度計は焙煎機の釜内の温度を測るために単調増加せず、豆投入時に温度が下がります)
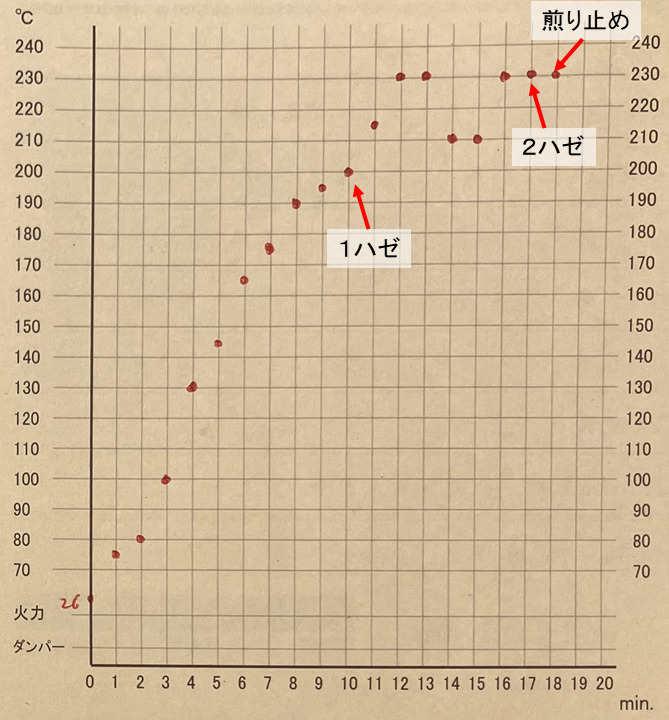
Fig.1 珈琲焙煎温度の時間変化の例
焙煎温度の測り方
焙煎中の珈琲豆の温度を測る方法は大きく分けて2種類あります。
一つ目は接触式の温度計(例えば熱電対)を焙煎釜に入れて測る方法があります。接触式の温度計は接触対象の正確な温度を測定できる点がメリットですが、一方で焙煎中の豆は撹拌されていて直接接触ができません。その代替として釜内部の気体温度を測定しますが、実際の豆の温度との乖離が起きるデメリットがあります。
二つ目はFig.1のグラフで用いた放射温度計を使用して測る方法です。Fig.2に示すように放射温度計は豆の温度を直接測定できる点がメリットですが、一方で測定対象物の放射率によって誤差を生じるデメリットがあります。
一般的に用いられる方法は一つ目の接触式の温度計を使用した方法です。釜内部の気体温度を測定する方法のため、豆の温度は焙煎士の経験で推測します。一方で私が用いているのは、最初に接触式の温度計を撹拌を止めた豆に接触させて温度を測定し、同時に放射温度計でも測定を行って放射率を決定します。以降は決定した放射率を用いて、放射温度計で豆を直接測定する方法です。

Fig.2 放射温度計を用いた珈琲豆温度の測定例
放射温度計のしくみ
それでは、放射温度計とはどのようなものなのでしょうか?
ハンドガンタイプの放射温度計の製品例(AD-5634,A&D社)をFig.3に示します。温度測定対象物に温度計の先端を向けてトリガを引くことで温度を測定することができます。この製品は測定データをmicroSDカードにcsv形式で自動保存できるため、記録の手間が省けてとても便利です。また、K型熱電対を接続して熱電対のデータも一緒に計測して保存できる機能も持っているため、熱電対の温度を用いて珈琲豆の放射率を決定する際に重宝しています。

Fig.3 放射温度計の製品例
放射温度計の先端が正確に対象物に向いていることを確認するために、ガイドレーザ(先端が向いている方向に出射するレーザ光)がついています。Fig.4は放射温度計の先端部を拡大した写真で、受光部(中央部の大きな開口部)とガイドレーザ出射部(上下二つの小さな開口部)が確認できます。

Fig.4 放射温度計の先端部
放射温度計の光学系をFig.5に示します。図の上方にあるのがガイドレーザの光学系で、図の下方にあるのが放射温度測定光学系です。ガイドレーザには赤色等の可視光半導体レーザが用いられ、コリメータレンズで平行光にビーム整形されて測定対象物に照射されます。対象物から放射された赤外線は対物レンズで集光されて、バンドパスフィルタを経由してフォトディテクタに入射します。バンドパスフィルタは測定に用いる波長の光だけを透過する効果があります。対物レンズには赤外線を透過する材料(Si/ZnS/Chalcogenaide等)が用いられます。フォトディテクタの信号はプリアンプ(Pre AMP)とアナログ・デジタルコンバータ(ADC)、放射率補正回路、リニアライザを経て表示器に温度として表示されます。
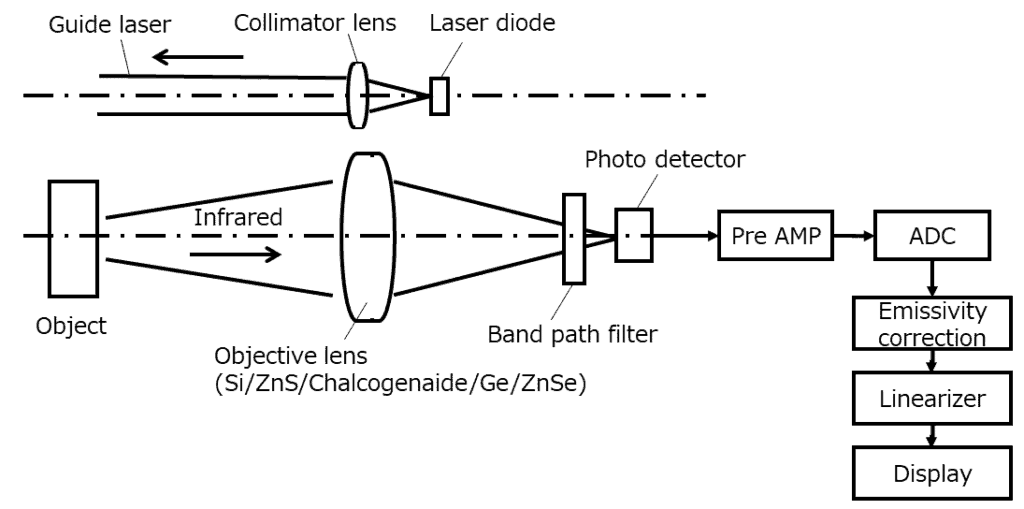
Fig.5 放射温度計の光学系
それでは,対象物から放射された赤外線はどのような原理で温度情報に変換されるのでしょうか?
物体はその温度に応じた電磁波(光)を放射します。その原理はプランクの法則とよばれる量子力学の基本法則で定式化されています。完全黒体(光を透過や反射をせず、すべて吸収する物体)の分光放射輝度はEq.1で表されます。
$$
L(\lambda,T)=\frac{2hc^{2}}{\lambda^{5}}\frac{1}{e^{\frac{hc}{\lambda k_{B}T}}-1} Eq.1\\
\begin{align}
&L(\lambda,T):分光放射輝度(W/sr/m^{2}/m)\\
&\lambda:電磁波の波長\\
&T:物体の温度\\
&h:プランク定数(6.63×10^{-34}(Js))\\
&c:光速(3.00×10^{8}(m/s))\\
&k_{B}:ボルツマン定数(1.38×10^{-23}(J/K))
\end{align}
$$
この式を用いて温度20℃~250℃において、分光放射輝度が波長0.3um~14.0umの範囲でどのような数値となるのかグラフにプロットしてみます。プロットに用いたpythonコードを以下に示します。実行にはjupyter notebookを使用しました。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as pltk
%matplotlib inline
c=3.00*10**(8)
h=6.63*10**(-34)
k=1.38*10**(-23)
T=np.array([293,323,373,423,473,523])
np_wl=np.arange(100,14001)
np_lmd=np_wl*10**(-9)
np_L20=(2*h*c**2)/(np_lmd**5*np.expm1(h*c/(np_lmd*k*T[0])))
np_L50=(2*h*c**2)/(np_lmd**5*np.expm1(h*c/(np_lmd*k*T[1])))
np_L100=(2*h*c**2)/(np_lmd**5*np.expm1(h*c/(np_lmd*k*T[2])))
np_L150=(2*h*c**2)/(np_lmd**5*np.expm1(h*c/(np_lmd*k*T[3])))
np_L200=(2*h*c**2)/(np_lmd**5*np.expm1(h*c/(np_lmd*k*T[4])))
np_L250=(2*h*c**2)/(np_lmd**5*np.expm1(h*c/(np_lmd*k*T[5])))
df_L=pd.DataFrame({'Wavelength':np_wl,'Lambda':np_lmd,'L(T:20)':np_L20,\
'L(T:50)':np_L50,'L(T:100)':np_L100,'L(T:150)':np_L150,\
'L(T:200)':np_L200,'L(T:250)':np_L250})
df_L.set_index('Wavelength',inplace=True)
fig,ax=plt.subplots(figsize=(10,10))
plt.plot(df_L['L(T:250)'],color='red',label='L(T:250℃)')
plt.plot(df_L['L(T:200)'],color='orange',label='L(T:200℃)')
plt.plot(df_L['L(T:150)'],color='gold',label='L(T:150℃)')
plt.plot(df_L['L(T:100)'],color='green',label='L(T:100℃)')
plt.plot(df_L['L(T:50)'],color='blue',label='L(T:50℃)')
plt.plot(df_L['L(T:20)'],color='Magenta',label='L(T:20℃)')
plt.xlabel("Wavelength[nm]",fontsize=16)
plt.ylabel("Spectral radiance[W/sr/m2/m]",fontsize=16)
plt.legend()
plt.grid()
ax.yaxis.set_major_formatter(pltk.ScalarFormatter(useMathText=True))
ax.ticklabel_format(style="sci", axis="y", scilimits=(8,8))プロットした結果をFig.6に示します。物体の温度が高くなるについれて放射輝度のピーク波長が短波長側にシフトしていることが分かります。これを「ウィーンの変位則」といいます。私達がこの仕組みを知る最も身近な存在は夜空に見える星です。温度の高い恒星ほど青白く、温度の低い恒星ほど赤く見えます。
以上を踏まえて、放射温度計では分光放射輝度を観測して温度を算出します。算出にあたって、低温域(1000℃以下)では波長10um付近、高温域(1000℃以上)では波長1um付近が用いられます。波長10umに着目すると、温度が20℃から250℃に変換するについれて非線形に放射輝度が上昇していることが分かります。この曲線を用いて、放射輝度から温度に換算します。

Fig.6 黒体の分光放射輝度
珈琲豆の放射率
放射輝度から温度に換算する上で放射率が重要なパラメータとなります。プランクの法則で導出された分光放射輝度は物質の持つ全放射エネルギーを100%放射した場合のものです。このように、すべての温度・波長に対して完全な放射を行うものを黒体と呼びます。ところが、実際の物体は黒体ではなく黒体よりも放射が少ないです。黒体に対する物体の放射発散度の比を放射率と定義してEq.2のように表します。
$$
\epsilon=\frac{M’}{M}=\frac{物体の放射発散度}{同一温度の黒体の放射発散度} Eq.2
$$
放射率はその物体の放射能力を表し、0<ε<1 の値をとります。全波長についての比率を全放射率、特定波長における比率を分光放射率といいます。放射率はその物体の吸収率αとほぼ等価であり,透過率τと反射率ρを用いてEq.3で表されます。これをキルヒホッフの法則といいます.
$$
\epsilon+\rho+\tau=\alpha+\rho+\tau=1 Eq.3
$$
このことから、吸収率が高い、すなわち、反射率と透過率の少ない物体ほど放射率が高いことが分かります。放射率は物体の状態(種類、表面状態)や測定条件(温度、角度、波長)によって変化します。光沢のある金属面は放射率が小さく、表面が酸化されると放射率が大きくなります。また、絶縁物は一般的に放射率が大きくなります。放射温度計ではこの放射率を用いて、対象物の放射輝度から黒体相当の放射輝度を算出し、実際の温度を導出します。
珈琲豆の焙煎で温度を測定するには、珈琲豆の放射率を知る必要があります。冒頭で述べたとおり、接触式の温度計で測定した温度を正とし、その温度と一致するように放射温度計の放射率設定を変化させて放射率を決定する方法を用いました。この実験で用いた器具をFig.7に示します。

Fig.7 放射率測定に用いた器具
Fig.8に珈琲豆の焙煎度に応じた放射率の関係を表しています。焙煎度が高くなるにつれて放射率が低下する傾向が見られました。見た目の色は黒く変化する一方で放射率が低下する(透過・反射率が上昇する)点は興味深いです。

Fig.8 焙煎度と放射率の関係
焙煎初期の放射率は0.98で、2ハゼの放射率は0.92でした。この結果の中央値を選択して、日頃の珈琲焙煎での温度測定では放射率0.95を用いています。
この実験ではざるを用いて焙煎を行っています。日頃の焙煎トレーニングから、火加減の調整や豆の撹拌が味作りにとても重要だと感じています。その結果として豆の温度の変化が観測されますので、豆の温度を測定することは味作りを定量的に制御する上で必要だと考えています。
おわりに
珈琲焙煎のトレーニングを始めたころは分からないことばかりでしたが、参考にさせていただいた本「中川ワニ著, “家でたのしむ手焙煎コーヒーの基本”, リトル・モア」がとてもよい足がかりになりました.また、焙煎を化学の視点で分析した本「旦部幸博, “コーヒーの科学”, 講談社」も参考になりました。著者は医学部の先生で、この本を通じて定性的な焙煎をより化学的な理論に基づいて行うきっかけになりました。
さらに、ベテラン焙煎士に焙煎指導をしていただきました。私の師匠は元刑事さんで、私の研究思考を見抜いてそれに合う指導をしてくれました。「ノウハウを教えるよりも、ご自身でじっくり考えて解を見出す方が良いと思います。私はその手助けをします。」と助言をいただき、焙煎を通じて自分自身のことも少し知ることができました。
このように、私にとっての珈琲は研究対象であり、人と人をつなぐツールであり、自分自身と向き合う時間を提供してくれる存在です。これからも、珈琲とともに過ごす時間を大切にしていきたいと思います。
参考文献
- “プランクの法則”, Wikipedia
- 井邊真俊, “赤外放射率の精密測定技術に関する調査研究”, 産総研計量標準報告, Vol.9, No.4, 2018
- “温度計測のFAQ”, 日本電気計測器工業会, https://www.jemima.or.jp
- 中川ワニ, “家でたのしむ手焙煎コーヒーの基本”, リトル・モア, 2018
- 旦部幸博, “コーヒーの科学”, 講談社


